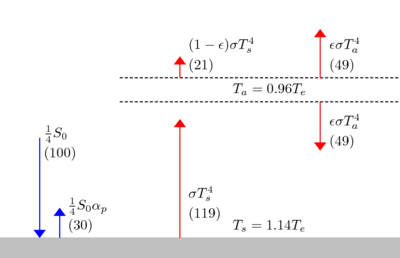
The greenhouse effect can be illustrated with an idealized planet. This is a common "textbook model" [1]: the planet will have a constant surface temperature Ts and an atmosphere with constant temperature Ta. For diagrammatic clarity, a gap can be depicted between the atmosphere and the surface. Alternatively, Ts could be interpreted as a temperature representative of the surface and the lower atmosphere, and Ta could be interpreted as the temperature of the upper atmosphere. In order to justify that Ta and Ts remain constant over the planet, strong ocean and atmospheric currents can be imagined to provide plentiful lateral mixing. Furthermore, any daily or seasonal cycles in temperature are assumed to be insignificant.
The model will find the values of Ts and Ta that will allow the outgoing radiative power, escaping the top of the atmosphere, to be equal to the absorbed radiative power of sunlight. When applied to a planet like Earth, the outgoing radiation will be longwave and the sunlight will be shortwave. These two streams of radiation will have distinct emission and absorption characteristics. In the idealized model, we assume the atmosphere is completely transparent to sunlight. The planetary albedo αP is the fraction of the incoming solar flux that is reflected back to space. The flux density of the incoming solar radiation is specified by the solar constant S0. For application to planet Earth, appropriate values are S0=1366 W m-2 and αP=0.30. Accounting for the fact that the surface area of a sphere is 4 times the area of its intercept (its shadow), the average incoming radiation is S0/4.
For short wave radiation, the surface of the Earth is assumed to have an emissivity of 1. All incident shortwave radiation is completely absorbed. The surface emits a radiative flux density F according to the Stefan-Boltzmann law:
- F = σT4
where σ is the Stefan-Boltzmann constant. A key to understanding the greenhouse effect is Kirchoff's law of thermal radiation. At any given wavelength the absorptivity of the atmosphere will be equal to the emissivity. Radiation from the surface could be in a slightly different portion of the infrared spectrum than the radiation emitted by the atmosphere. The model assumes that the average emissivity (absorptivity) is identical for either of these streams of infrared radiation, as they interact with the atmosphere. Thus, for longwave radiation, one symbol ε denotes both the emissivity and absorptivity of the atmosphere, for any stream of infrared radiation.

The infrared flux density out of the top of the atmosphere:
In the last term, ε represents the fraction of upward longwave radiation from the surface that is absorbed, the absorptivity of the atmosphere. In the first term on the right, ε is the emissivity of the atmosphere, the adjustment of the Stefan-Boltzmann law to account for the fact that the atmosphere is not optically thick. Thus ε plays the role of neatly blending, or averaging, the two streams of radiation in the calculation of the outward flux density.
Zero net radiation leaving the top of the atmosphere requires:
Zero net radiation entering the surface requires:
Energy equilibrium of the atmosphere can be either derived from the two above equilibrium conditions, or independently deduced:
Note the important factor of 2, resulting from the fact that the atmosphere radiates both upward and downward. Thus the ratio of Ta to Ts is independent of ε:
Thus Ta can be expressed in terms of Ts, and a solution is obtained for Ts in terms of the model input parameters:
or
The solution can also be expressed in terms of the effective emission temperature Te, which is the temperature that characterizes the outgoing infrared flux density F, as if the radiator were a perfect radiator obeying F=σTe4. This is easy to conceptualize in the context of the model. Te is also the solution for Ts, for the case of ε=0, or no atmosphere:
With the definition of Te:
For a perfect greenhouse, with no radiation escaping from the surface, or ε=1:
Using the parameters defined above to be appropriate for Earth,
For ε=1:
For ε=0.78,
 .
.
This value of Ts happens to be close to a very widely quoted (but unattributed) 288 K claimed for the average global "surface temperature". ε=0.78 implies 22% of the surface radiation escapes directly to space, consistent with the statement of 15% to 30% escaping in the greenhouse effect.
The radiative forcing for doubling carbon dioxide is 3.71 W m-2, in a simple parameterization. This is also the value endorsed by the IPCC. From the equation for  ,
,
Using the values of Ts and Ta for ε=0.78 allows for  = -3.71 W m-2 with Δε=.019. Thus a change of ε from 0.78 to 0.80 is consistent with the radiative forcing from a doubling of carbon dioxide. For ε=0.80,
= -3.71 W m-2 with Δε=.019. Thus a change of ε from 0.78 to 0.80 is consistent with the radiative forcing from a doubling of carbon dioxide. For ε=0.80,
Thus this model predicts a global warming of ΔTs = 1.2 K for a doubling of carbon dioxide. A typical prediction from a GCM is 3 K surface warming, primarily because the GCM allows for positive feedback, notably from increased water vapor. A simple surrogate for including this feedback process is to posit an additional increase of Δε=.02, for a total Δε=.04, to approximate the effect of the increase in water vapor that would be associated with an increase in temperature. This idealized model then predicts a global warming of ΔTs = 2.4 K for a doubling of carbon dioxide, roughly consistent with the IPCC.

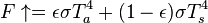

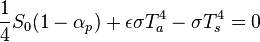


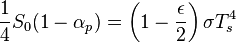
![T_s=\left[ \frac{S_0(1-\alpha_p)}{4\sigma} \frac{1}{1-{\epsilon \over 2}} \right]^{1/4}](http://upload.wikimedia.org/math/f/6/0/f60ed5667aa5d6059ec21d6d485c6e73.png)
![T_e \equiv \left[ \frac{S_0(1-\alpha_p)}{4\sigma} \right]^{1/4}](http://upload.wikimedia.org/math/a/a/8/aa849874c11f621aa0ca3c9c3cc99c2d.png)
![T_s= T_e \left[ \frac{1}{1-{\epsilon \over 2}} \right]^{1/4}](http://upload.wikimedia.org/math/a/9/a/a9aef1253eb6921fd553b60e19c8e381.png)




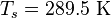

No comments:
Post a Comment